Measuring dependency
A transcript of measuring dependency presentation, by Rebecca Pillinger
- To watch the presentation go to Measuring Dependency - voice-over with slides and subtitles (If you experience problems accessing any videos, please email info-cmm@bristol.ac.uk)

The question of the relative sizes of the level one and level two variance is very relevant to our decision to use multilevel modelling. That's because the relative sizes change according to how much dependency we have in our data. And the dependency comes about because observations from the same group are likely to be more similar than those from different groups. So, for example, if we have exam results for pupils from the same school, those are likely to be more similar than exam results for pupils from different schools, and if we measure the heights of children from the same family, those are likely to be more similar than the heights of children from different families. And the fact that we have dependent data is the whole reason that we're using multilevel modelling. And that's partly because multilevel modelling will correctly estimate the standard errors for our parameters. If we use a single level model for dependent data, then the standard errors will be underestimated.

So as an example of that, we compare a single level and a multilevel model here. So you can see the models in the purple box; we've got the single level model at the top, and below that the two level model; and we're fitting these models to the data in the tutorial worksheet that's supplied with MLwiN.
So if you look at the estimate for the coefficient for boys' school, for the single level model you can see that the parameter estimate, 0.122, is more than twice the standard error, 0.049. So if we fit a single level model, then we'll find that the coefficient for boys' school is significant. But if you look at the estimates for the multilevel model, the parameter estimate, 0.12, is clearly not more than twice the standard error, 0.149, so if we fit a multilevel model, then we will not find that the coefficient for boys' school is significant. So there's quite a difference there in the interpretation of our findings, depending on whether we fit a single level model or a multilevel model. And for girls' school as well, although we will find that the coefficient is significant for both models, for the single level model, clearly it meets a higher degree of significance, so again, there's an important difference there. And the key point here is that the single level model is actually giving us the wrong values for the standard errors. So this is a clear reason why we should use the multilevel model, so that we will get the correct answers and we'll be able to correctly identify which coefficients are significant.

So, we're using multilevel modelling because we have dependent data, and therefore we would like to know how much dependency we actually have in our data.

And we can use the variance partitioning coefficient to measure this dependency; this is also called the VPC, or rho, or the intraclass correlation. And for the two level random intercepts case, we can calculate it using this formula
[formula for rho]
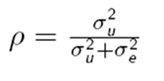
so it's the level two variance divided by the total variance, which is the level two variance plus the level one variance. It's important to be careful, because the VPC is actually similar to, but not the same as, the shrinkage factor, which we use in calculating residuals.
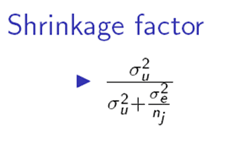
So here's the shrinkage factor, down in the bottom left, and you can see that the shrinkage factor actually has the level one variance divided by n_j, the number of elements in the group, so that's the important difference from the VPC,

you can see that we don't have that divided by n_j for the VPC, so it's important to keep those two separate and not get confused.
So the VPC is the proportion of the total variance that's at level two. How do we actually interpret that?
Large value of rho:

Well, let's have a look at an example of a situation where rho is big. So here the group lines are quite spread out around the overall regression line, but the individual data points are not very spread out around their group lines. So here, the level two variance- the variance of the group lines- is big, but the level one variance- the variance around the group lines- is small.
So if we look at the formula [for rho] again, you can see that we've got something big divided by something big plus something small, so that's going to be close to 1, and that's a large value for rho.
So let's have a look again: that's what a large value of rho looks like.
The other case is a small value of rho. So now the group lines are less spread out around the overall regression line, so the level two variance is smaller, but this time the individual data points are very spread out around their group lines, so the level one variance is large.
So if we look at the formula [for rho] again: so we have something small divided by something small plus something big, so that means that rho is going to be quite close to zero, and that's a small value for rho. So let's look at that again:

that's a small value for rho.
So if we look at the formula [for rho] , we can actually see that the biggest that rho can possibly be is 1, and the smallest it can possibly be is zero. We won't in practice expect to find a value of 1 or zero for rho, but from a theoretical point of view it's quite interesting to actually have a look at what values of 1 or zero would look like on a graph. So let's look at a value of 1 first. So when rho is 1, the top and bottom of that formula must be equal, so that means the level one variance must be zero and we have

this situation: the level one variance is zero, so the individual points are not at all spread out around their group lines, they all lie exactly on the group lines. The level two variance, on the other hand, still exists, so the group lines are still spread out around the overall regression line. And this is the situation of total dependency, because once we know the value of the x variable for a data point, and we know which group it belongs to, we've totally determined its y-value. And obviously in practice that doesn't tend to happen in the social sciences; this is just a theoretical situation.
The other situation we want to look at is when rho is zero, and in that case the top of that formula [for rho] must be zero, so the level two variance is zero. So in that case

we're going to have this situation- we'll build it up gradually so you can see what's going on- the group lines must all lie on the overall regression line, there's no level two variance so they're not spread out around it. But the individual data points are still spread out around their group lines, because there is still level one variance. And note that the groups can differ from each other in terms of their x variables, so for example the red group seems to have values for the x variable that are towards the low end of the scale, while the blue group seems to have values for the x variable that are towards the high end of the scale; but if we have included the x variable in our model, then adding in the group doesn't tell us anything extra about the value of the y variable for the data point. So if we haven't put in the x variable to our model, then the group can tell us something about the value of the y variable, because the group tells us something about the value of the x variable, and that tells us something about the value of the y variable, but if we have put in the value of the x variable, then adding in the group that the data point comes from doesn't give us anything extra. So here we have no dependency. And that means that if we wanted, we could use a single level model. Now of course in practice, we don't expect to find a value of exactly zero for rho. But we may find values that are close enough that we can use a single level model.

So we've seen from the formula that rho always lies between zero and 1, and we've also seen that we don't expect to actually find a value of zero or 1. So a question we can ask is, in practice, what is a large value for rho: what kind of things can we expect to find? Well, it turns out that in practice 0.3 is a large value for rho in the social sciences, which indicates a lot of dependency in the data. So, as an example of how to interpret rho, when rho is 0.3, roughly one third of the variation is between groups, so two thirds of the variation is within groups. And that actually shows another important value of rho: that it can tell us what proportion of the variation is at these different levels. And that's useful because that's telling us something about how the values of the y variable come about: to what extent are they determined by the group and to what extent are they determined by the individual?
So basically, rho is a very useful measure.